欧美色盟,色婷婷AV一区二区三区之红樱桃,亚洲精品无码一区二区三区网雨,中国精品视频一区二区三区

2022年5月13日，Wiley Interdisciplinary Reviews-Computational Molecular Science雜志在線發表了北京大學化學與分子工程學院劉劍課題組的題為“New Phase Space Formulations and Quantum Dynamics Approaches”的邀稿文章。

在牛頓經典力學框架下，分子系統的所有物理和化學觀測量都可以在由粒子位置和動量組成的相空間中描述，動力學由相空間中的經典軌跡刻畫。然而，自然界本質上由量子力學支配。當分子系統的量子力學特性顯現時，海森堡不確定原理表明粒子的位置和動量并不能夠同時被精確確定，經典力學無法勝任。

Eugene Wigner（1963年諾貝爾物理學獎得主）在1932年提出了量子力學的一種等價表示形式—相空間表示理論，建立了量子算符和位置-動量相空間函數的一一映射關系。量子相空間理論有方便的量子-經典對應關系，在量子力學表述和量子系統含時演化等方面得到了大量應用。在量子相空間中容易引入軌跡近似，從而能夠勝任大體系的線性標度近似計算，為研究復雜大分子和溶液、固體等凝聚相體系量子性質提供一種有效計算手段。Wigner相空間本質是無限邊界相空間，適用于研究連續自由度的量子體系。

由于原子核和電子的質量相差至少在3個量級以上，原子核和電子的運動尺度一般可以分離，即玻恩-奧本海默近似成立。此時，分子體系不涉及電子態的躍遷，稱為絕熱體系。針對絕熱體系，位置-動量相空間理論在原子核量子效應的應用研究已經表現出優勢。與之相比，經典分子動力學無法準確描述低溫或含氫原子的分子體系；而這些復雜分子體系的原子核量子本征能級十分稠密，波函數表示理論的計算代價巨大。劉劍課題組近年來基于Wigner量子相空間發展出的平衡連續性動力學（ECD）與路徑積分劉維爾動力學（PILD）方法能夠在保證經典極限、高溫極限和諧振子極限嚴格成立的前提下，保證含時演化過程中量子平衡分布不變，為給定溫度的復雜分子系統提供更為可靠的量子動力學模擬手段。相空間量子動力學方法已經應用到水、氨、甲烷、甲醛、過氧化氫和液態水等體系的紅外振動光譜和拉曼振動光譜的模擬。結合機器學習擬合技術，計算效率能夠進一步提升，有望直接應用到更復雜分子體系的核量子效應模擬。

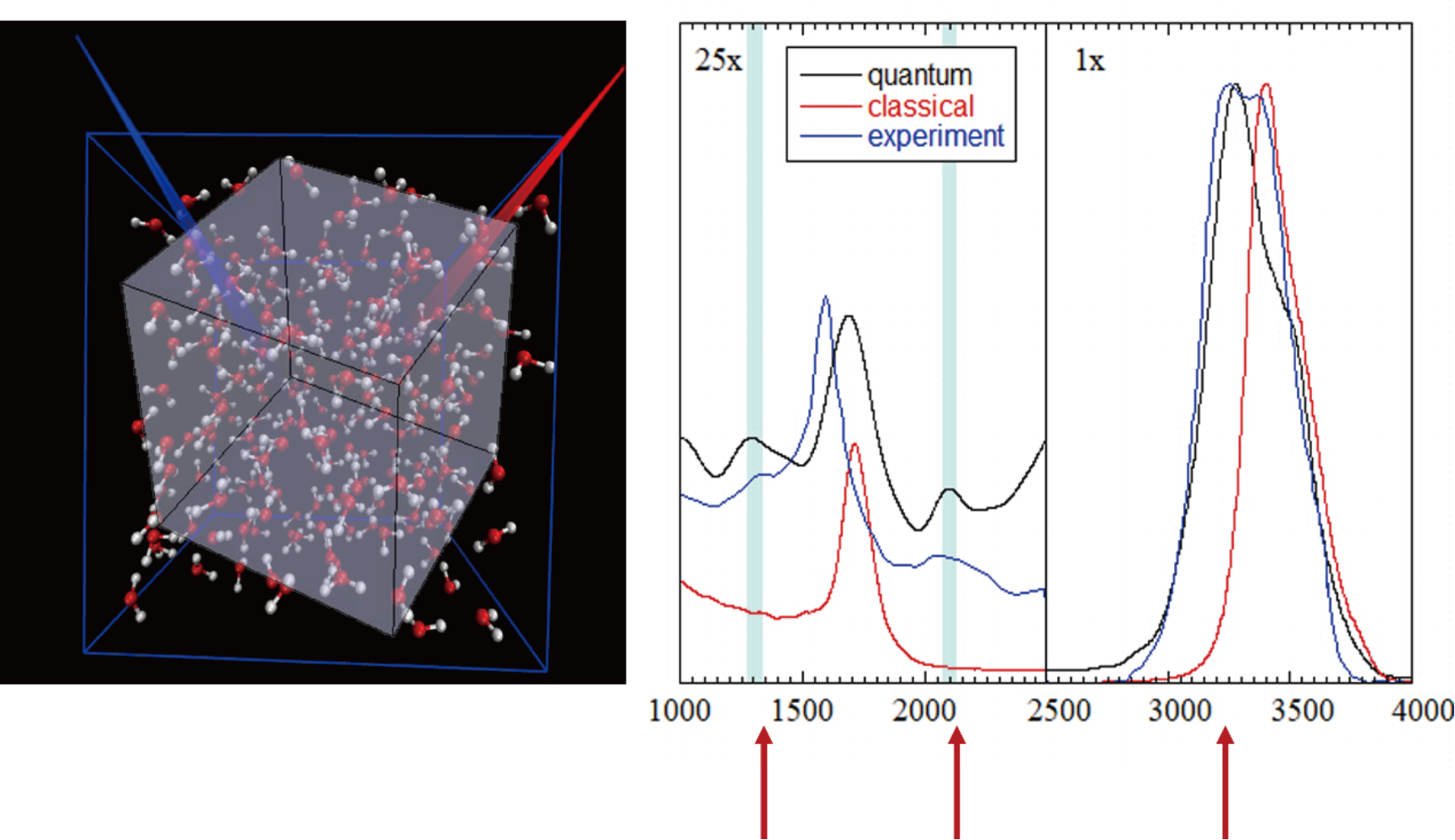
圖1：采用Wigner相空間的軌線動力學方法對于液相水拉曼光譜的模擬結果。

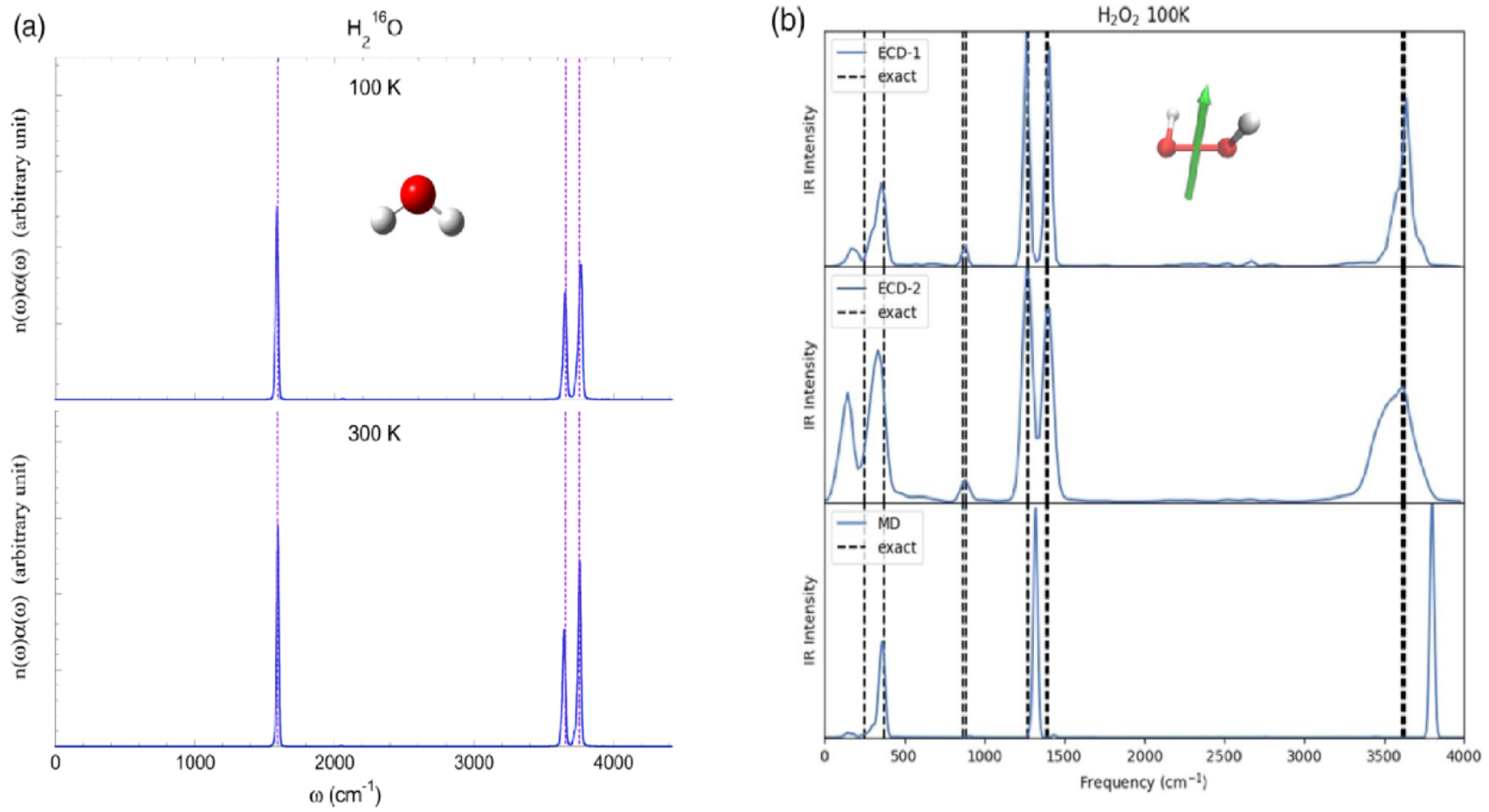
圖2：基于Wigner相空間的軌線動力學對于水/過氧化氫分子紅外光譜的模擬結果。

當原子核和電子的運動尺度不可分離時，即玻恩-奧本海默近似不成立，分子體系涉及電子態之間的無輻射躍遷，稱為非絕熱體系。很多光化學和光物理過程（例如，光合作用、光異構化反應、光催化反應、激發態質子轉移、電子轉移反應、電子能量轉移、載流子輸運、激子裂分和分離等）牽涉到原子核和電子的耦合運動，必須發展和應用非絕熱量子動力學方法才能進行定量研究。由于非絕熱體系的哈密頓算符既包含連續自由度（原子核自由度）也包含離散自由度（電子態自由度），傳統的位置-動量相空間表示理論亟需進一步發展。

基于2016年的映射哈密頓模型的統一框架，劉劍課題組在2019年首次從電子態布居數之和為1這個必須滿足的物理要求出發，將其作為約束條件建立非絕熱體系的相空間映射動力學，并后續發展了只含有限數目量子態的離散系統和約束（位置-動量）相空間的一一對應關系。電子態自由度的約束位置-動量相空間和原子核自由度的Wigner相空間相結合可以給出非絕熱體系量子性質在廣義位置-動量相空間中的嚴格表達形式。由哈密頓算符在廣義位置-動量相空間中的經典映射模型（CMM）可以推導出軌跡運動方程，作為量子相空間劉維爾動力學方程的近似。CMM動力學方法對一系列模型測試體現了其描述非絕熱動力學的優點，能夠超越目前被廣泛使用的面跳躍（surface hopping）和平均場（也稱為Ehrenfest動力學）方法。最近的工作里，劉劍課題組將原先基于單一γ因子的映射相空間擴展到使用兩個（或多個）γ因子的組合，發展出了新的核與電子統一的映射位置-動量相空間形式，稱為加權映射模型（wMM）。圖3展示了wMM和CMM對于γ因子的選擇比較，以及用于量子糾纏態的可視化表示結果。圖4展示了wMM應用于非絕熱體系的結果。數值結果表明CMM/wMM在自旋玻色模型（圖4a）、原子-光腔相互作用模型（圖4b）等體系中，其長時描述都要優于平均場動力學/面跳躍動力學的結果；在Tully的一維散射模型（圖4c）中，wMM數值表現良好，尤其是ECR散射問題上，wMM能夠準確捕捉到階型曲線，更超越了原先的CMM/平均場動力學/面跳躍動力學的數值表現。而在吡嗪分子的錐型交叉問題上（圖4d），CMM/wMM可以克服Ehrenfest動力學的不足。

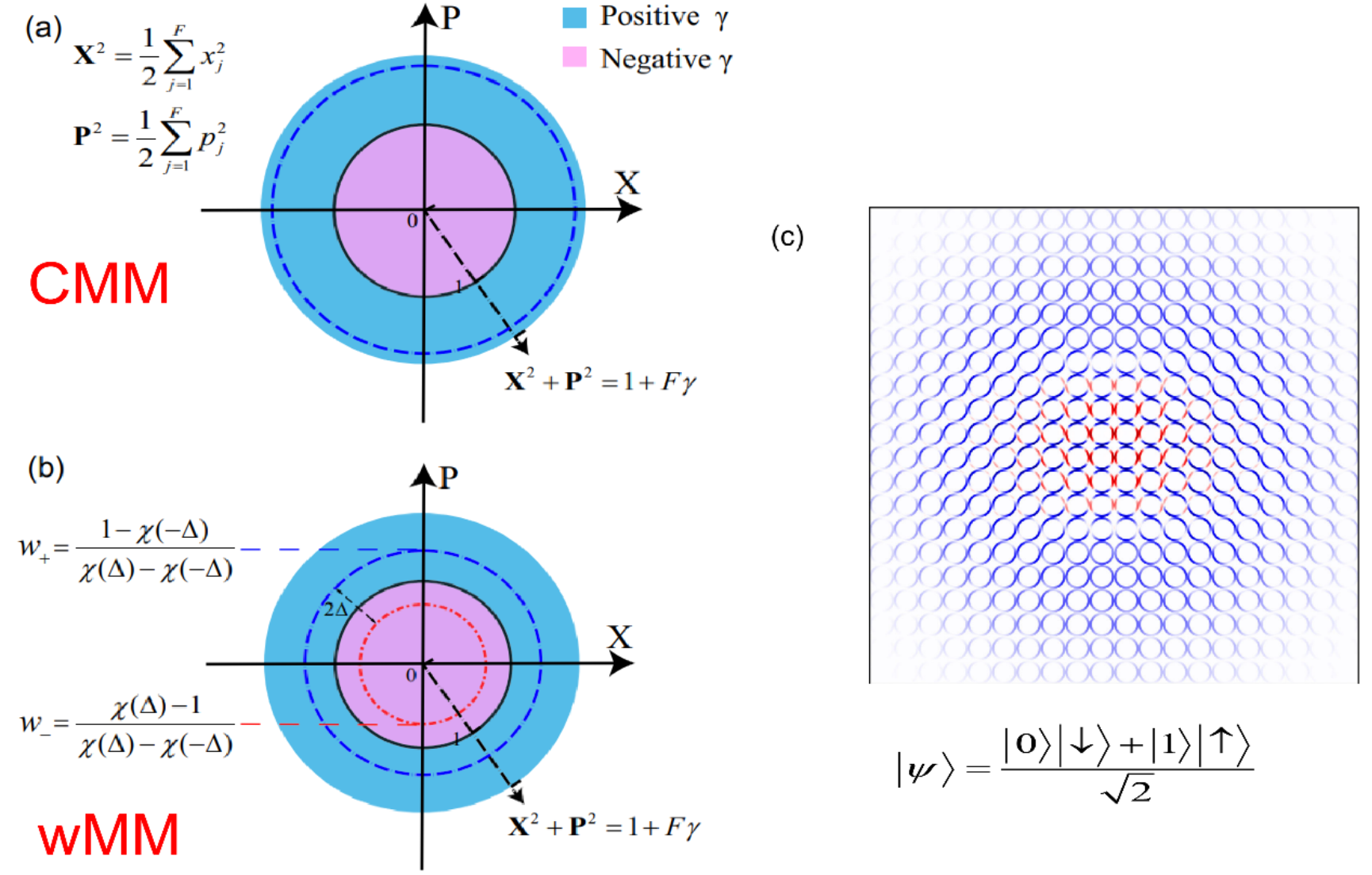
圖3：(a)-(b)分別為電子態映射的約束位置-動量相空間CMM和wMM的示意圖。(c)是對于核與電子的混合比特的相空間可視化示意圖，其中原子核采用了Wigner相空間而電子態采用了wMM相空間。

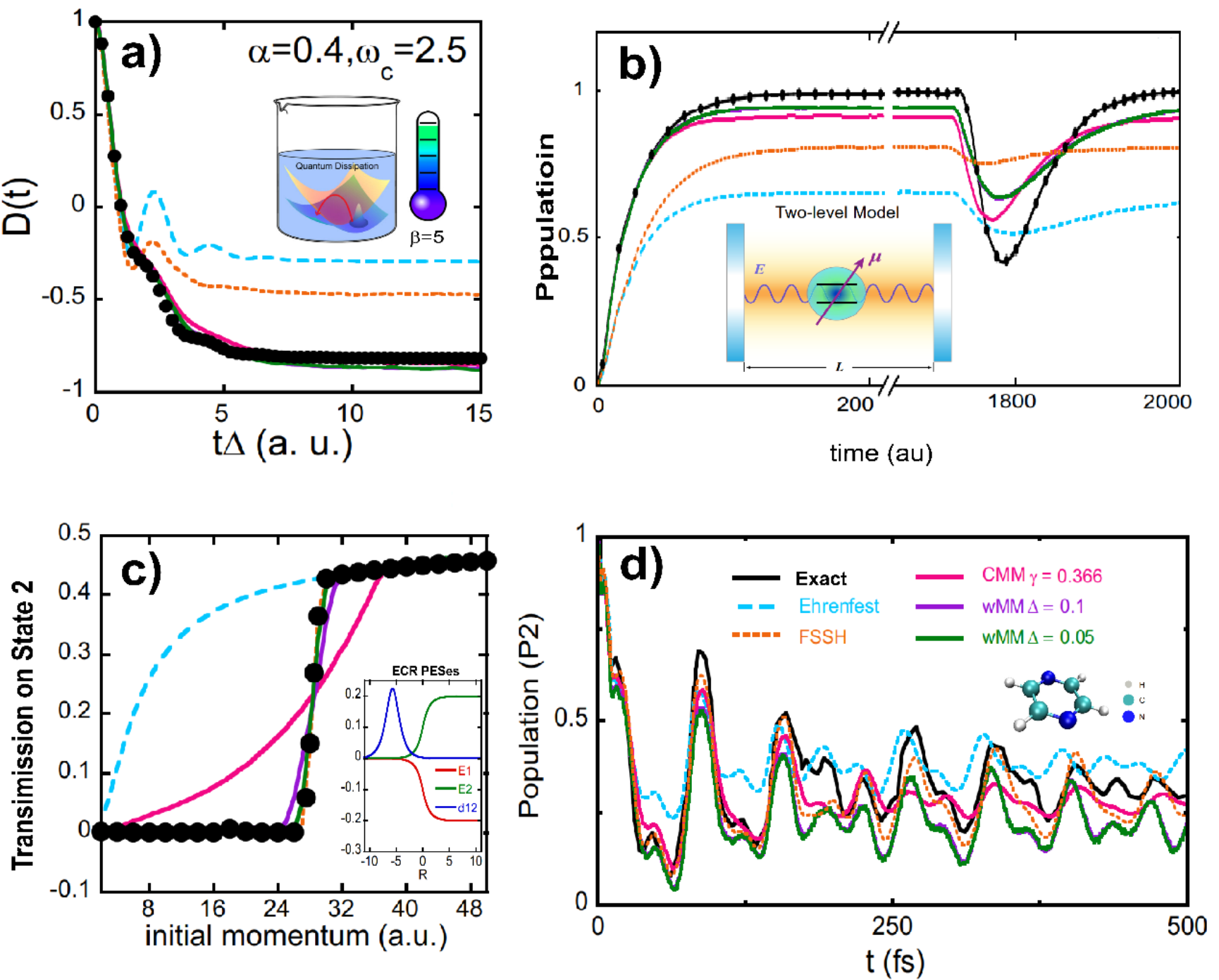
圖4：原子核的Wigner相空間和電子態的wMM相空間相結合應用于一系列非絕熱問題的計算。

                                                           (a)(b)(c)(d)分別展示了自旋玻色模型、原子-光腔自發輻射模型、Tully的ECR模型以及吡嗪錐形交叉模型的計算結果。

此外，該文整理了劉劍課題組前期一系列工作中對于電子態絕熱表象和透熱表象的相空間運動方程等價關系的推導，關于約束位置-動量相空間和Stratonovich相空間的關系討論，關于量子劉維爾方程在廣義位置-動量相空間的表示形式和近似，等等。

綜上，劉劍課題組發展了無限邊界的位置-動量相空間表示理論中的軌線量子動力學方法，同時滿足對諧振子體系（包含非線性算符的）時間關聯函數的準確處理以及平衡系統統計力學物理量不隨時間變化這兩個最基本物理要求，為動力學物理量的計算提供更可靠手段，并已應用于實際體系振動光譜的研究；提出和發展了包含了有限數目離散態的量子體系的約束位置-動量相空間表示理論，在統一框架下，發展基于軌線的非絕熱量子動力學方法（CMM和wMM），并應用到氣態和凝聚態非絕熱分子體系。該文展示了廣義位置-動量相空間表示理論和對應的軌跡近似方法有望于在熱化學、光化學的實際凝聚態復雜分子體系的理論研究中提供有效研究手段。

北京大學化學與分子工程學院的三年級研究生賀鑫和吳柏華是這篇文章的共同第一作者，四年級本科生尚游皓和李炳其、一年級研究生程祥松參與貢獻，劉劍研究員為通訊作者。該工作得到了國家自然科學基金委、科技部、北京分子科學國家研究中心、化學與分子工程學院的資助。計算資源由北京并行科技、廣州超級計算中心以及北京大學高性能計算平臺提供。

論文信息：

New Phase Space Formulations and Quantum Dynamics Approaches. Xin He, Baihua Wu, Youhao Shang, Bingqi Li, Xiangsong Cheng, Jian Liu. Wiley Interdisciplinary Reviews Computational Molecular Science, e1619 (2022)

https://doi.org/10.1002/wcms.1619

期刊介紹：

Wiley Interdisciplinary Reviews-Computational Molecular Science于2011年創刊，由Wiley出版社出版，為理論與計算分子科學領域的權威綜述期刊，內容涵蓋理論與計算分子科學的各個熱門方向。2021年影響因子達到25.113。

參考資料：https://www.chem.pku.edu.cn/kyjz/140667.htm